Machine Translation: Statistical approach
Back to Introduction, Rule-based systems or forward to Evaluation.
Introduction
- SMT inspired by information theory and statistics
- used by big players Google, IBM, Microsoft
- millions of webpages translated with SMT daily
- gisting: we don’t need exact full translation
- pre-translating in CAT
- trending right now: neural network models for MT
Words
- usually, the basic unit = word
- lowercase vs. original-case input
- the makes up 7% of English texts
- top 10 words ~ 30% of all texts
- issues: typos, proper names, loanwords →
out-of-vocabulary (OOV), zero-frequency , rare words
Sentences
- syntactic structure differs in various languages
- inserting of functional words (the, punctuation)
- rearranging:
er wird mit uns gehen → he will go with us - some phenomena can not be translated on the sentence level: anaphora
- level of document: theme (topic) can help with WSD
- one sense per discourse: bat != pálka in zoology
Parallel corpora I
- basic data source
- available sources ~10–100 M
- size depends heavily on a language pair
- multilingual webpages (online newspapers)
- paragraph and sentence alignment needed
- Kapradí, Shakespeare, various translators (FI+FF)
- InterCorp manually aligned fiction books (ČNK, FF UK)
- e-books
Parallel corpora II
- Linguistics Data Consorcium (LDC):
Arabic-English, Chinese-English, Gigaword corpus (English, 7 Gw) - Europarl: 11 ls, 40 M words
- OPUS: parallel texts of various origin, open subtitles, UI localizations
- Tatoeba: sentences for language learners
- Acquis Communautaire: law documents of EU (20 ls)
- Hansards: 1.3 M pairs of text chunks from the official records of the Canadian Parliament
- EUR-Lex
Translation memories
- the same structure as par. corpora
- different terminology: segments (blocks in docx)
- usually in XML: TMX / XLIFF
- can store formatting
- valuable but usually commercial (not available)
- DGT
- MyMemory
Comparable corpora
- texts from the same domain, not translations:
New York Times, Le Monde - Koehn on comparable corpora
- Wikipedia language mutations
- bilingual web pages
- for document level statistics
- useful for extracting bilingual dictionaries and terminologies (in-domain)
- Bilingual document alignment
- Pseudo-parallel corpus from Wikipedia (A. Štromajerová)
Sentence alignment
- sometimes sentences are not in 1:1 ratio in corpora
- some languages do not explicitly delimit sentence boundaries (Thai)
- It is small, but cozy. Es is klein. Aber es ist gemütlich.
| P | alignment |
|---|---|
| 0.89 | 1:1 |
| 0.0099 | 1:0, 0:1 |
| 0.089 | 2:1, 1:2 |
| 0.011 | 2:2 |
Church-Gale alignment
- paper in Computational linguistics
- only lengths are considered
- implementations in Python, C (in the paper), NLTK
- (almost) language independent
Hunalign
- Church-Gale with a dictionary
- dictionary predefined
- or statistically computed from length-based alignment
Comparison of sentence aligners
- Hunalign, Gale-Church
- Bilingual Sentence Aligner (Moore, 2002): first pass with cognates, lengths, second pass with IBM-1
- Gargantua: like BSA, works with 1:N/N:1 alignments
- GMA: word correspondence, only cognates
- Bluealign scored best in extrinsic eval. (MT)
- GSA+: cognates, anchor word list
- TCA: lengths, cognates, anchor word list
Probability and statistics basics for SMT
Zipf’s law
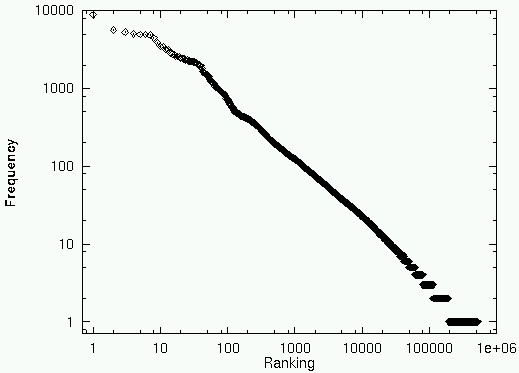
$r$ rank, $f$ = word freq., $c$ = constant; $r \times f = c$
Probability distribution
- a graph of probability values for elementary phenomena of a random variable
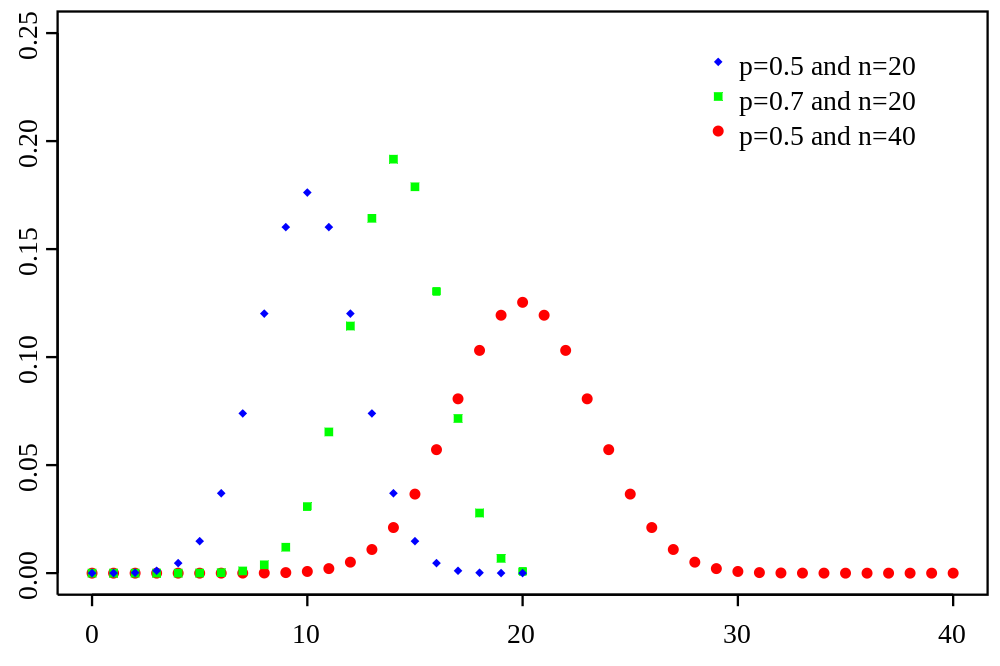
- uniform: roll of dice, coin (discrete variable)
- binomial: multiple roll (quincunx) $$b(n, k; p) = {n \choose k} p^k (1-p)^{n-k}$$
Binomial distribution
Statistics
- random variable, probability function, etc.
- we have data, we want to get distribution describing the data best
- law of large numbers: the more data we have the better we are able to guess its probability distribution
- roll of a loaded dice; $\pi$, $e$ calculation
- independent variables: $\forall x, y: p(x, y) = p(x) . p(y)$
- joint probability: roll of dice and coin: $p(6, \mbox{heads})$
- conditional probability: $p(y|x) = \frac{p(x, y)}{p(x)}$
for independent variables: $p(y|x) = p(y)$
Conditional probability
Bayes’s rule
$$p(x|y) = \frac{p(y|x) . p(x)}{p(y)}$$
- example with the dice
- $p(x)$ prior
- $p(y|x)$ posterior
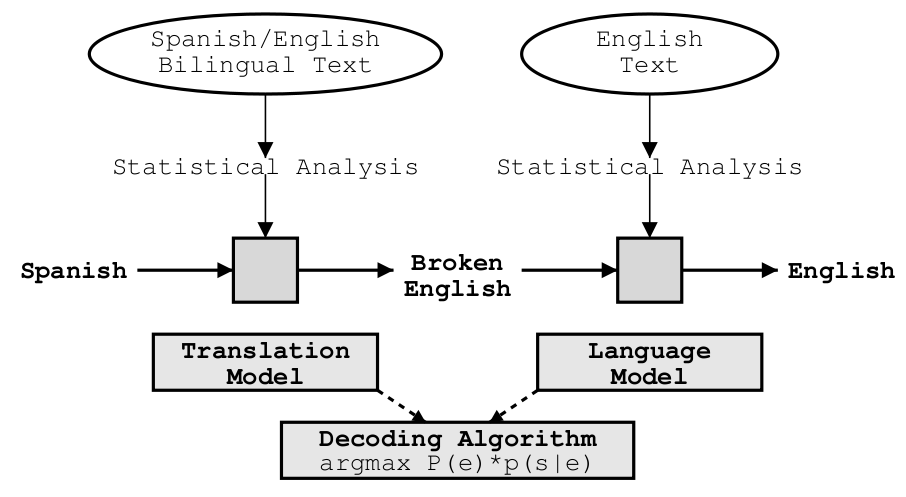
SMT noisy channel principle
Claude Shannon (1948), self-correcting codes transfered through noisy channels based on information about the original data and errors made in the channels.
Used for MT, ASR, OCR. Optical Character Recognition is erroneous but we can estimate what was damaged in a text (with a language model); errors l$\leftrightarrow$1$\leftrightarrow$I, rn$\leftrightarrow$m etc.
$$e^* = \arg\max_e p(e|f)$$ $$= \arg\max_e \frac{p(e)p(f|e)}{p(f)}$$ $$= \arg\max_e p(e)p(f|e)$$
Reformulation of MT formula
$$e^* = \arg\max_e \sum_{m=1}^M \lambda_m h_m (e, f)$$
(Och et al., 2004)
SMT components
Language model
- how we get $p(e)$ for any string $e$
- the more $e$ looks like proper language the higher $p(e)$ should be
- issue: what is $p(e)$ for an unseen $e$?
Translation model
- for $e$ and $f$ compute $p(f|e)$
- the more $e$ looks like a proper translation of $f$, the higher $p(f|e)$
Decoding algorithm
- based on TM and LM, find a sentence $f$ as the best translation of $e$
- as fast as possible and with as few memory as possible
- prune non-perspective hypotheses
- but do not lost any valid translations
Language models
Noam Chomsky, 1969:
But it must be recognized that the notion “probability of a sentence” is an entirely useless one, under any known interpretation of this term.
Fred Jelinek, 1988, IBM:
Anytime a linguist leaves the group the recognition rate goes up.
What is it good for?
What is the probability of utterance of $s$?
I go to home vs. I go home
What is the next, most probable word?
Ke snídani jsem měl celozrnný …
{chléb $>$ pečivo $>$ zákusek $>$ mléko $>$ babičku}
Language models probability of a sentence
- we look for a probability of a following word
- LM is probability distribution over all possible word sequences
Probability of word sequences
$p_{LM}(\hbox{včera jsem jel do Brna})$
$p_{LM}(\hbox{včera jel do Brna jsem})$
$p_{LM}(\hbox{jel jsem včera do Brna})$
Chomsky was wrong
Colorless green ideas sleep furiously
vs.
Furiously sleep ideas green colorless
LM assigns higher p to the 1st! (Mikolov, 2012)
LM for fluency and WSD
- LMs help ensure fluent output (proper word order)
- LMs help with WSD in general cases
- if a word is polysemous, we can choose the most frequent translation (pen → pero)
- LMs help with WSD using a context
N-gram models
- n-gram is a very useful concept in NLP
- it uses statistical observation of input data
- two applications in machine translation:
- what follows after I go? home is more frequent than house
- I go to home × I go home
Generating random text
To him swallowed confess hear both. Which. Of save on trail for are ay device and rote life have Every enter now severally so, let. (unigrams)
Sweet prince, Falstaff shall die. Harry of Monmouth’s grave. This shall forbid it should be branded, if renown made it empty. (trigrams)
Can you guess the author of the original text?
N-grams: chain rule
$W = w_1, w_2, \cdots, w_n$
$$p(W) = \prod_{i=1}^n p(w_n | w_1 \dots w_{n-1})$$
$$= p(w_1)p(w_2|w_1)p(w_3|w_1,w_2)\dots p(w_n|w_1\dots w_{n-1})$$
- no data for majority of $w_i, \dots, w_j$
- → data sparsity / sparseness
- the goal is to generalize observed data
Markov’s chain, process, assumption
Since $p$ is not available for longish word sequences, we limit the history to $m$ words using Markov’s assumption
$p(w_n|w_1 \dots w_{n-1}) \simeq p(w_n|w_{n-m+1} \dots w_{n-2} w_{n-1})$
For guessing a following word it is sufficient to consider ($m-1$) preceding words. $m$ is order of a model.
Usually 3- to 5-grams.
Maximum likelihood estimation
$$p(w_3|w_1,w_2) = \frac{count(w_1, w_2, w_3)}{\sum_w count(w_1, w_2, w)}$$
(the, green, *): 1,748× in EuroParl
| w | count | p(w) |
|---|---|---|
| paper | 801 | 0.458 |
| group | 640 | 0.367 |
| light | 110 | 0.063 |
| party | 27 | 0.015 |
| ecu | 21 | 0.012 |
Maximum likelihood principle
$$ P(\mbox{chléb}|\mbox{ke snídani jsem měl celozrnný}) $$ $$= {{|\mbox{ke snídani jsem měl celozrnný chléb}|} \over{|\mbox{ke snídani jsem měl celozrnný}|}}$$
LM quality
We need to compare quality of various LMs.
2 approaches: extrinsic and intrinsic evaluation.
A good LM should assign a higher probability to a good (looking) text than to an incorrect text. For a fixed testing text we can compare various LMs.
Extrinsic evaluation
- do not assess the quality of LM on its own
- use it in an application
- MT, OCR, ASR, text compression, …
- compare the outcomes for various LMs
Entropy
- from physics to theory of information
- Shannon, 1949
- the expected value (average) of the information contained in a message
- information viewed as the negative of the logarithm of the probability distribution
- information is a non-negative quantity
- events that always occur do not communicate information
- pure randomness has highest entropy (uniform distribution $log_2 n$)
$E(X) = -\sum_{i=1}^n {p(x_i) \log_2 p(x_i)}$
- poses limits for data compression
- data can’t be compressed more than its entropy allows
- entropy of language data (redundancy)
- cca 1.1 bit per character (English)
- redundancy?
- Hutter Prize
- minimalization of redundancy = AI
Cross-entropy
$$H(p, q) = -\sum_x p(x), \log q(x)$$
$$\begin{align*} H(p_{LM}) &= -\frac{1}{n} \log p_{LM}(w_1, w_2, \dots w_n)\ &= - \frac{1}{n} \sum_{i=1}^{n} \log p_{LM}(w_i|w_1, \dots w_{i-1}) \end{align*}$$
Corresponds to a measure of uncertainty of a probability distribution when predicting true data. The lower the better.
The second formula is a Monte Carlo estimate of the true cross entropy.
A good LM should reach entropy close to a real entropy of language. That can not be measured but quite reliable estimates do exist, e.g. Shannon’s game.
Perplexity
$$PP = 2^{H(p_{LM})}$$
$$PP(W) = p(w_1 w_2 \dots w_n)^{-{1\over N}}$$
A good LM should not waste $p$ for improbable phenomena. The lower entropy, the better $\rightarrow$ the lower perplexity, the better.
Minimizing probabilities = minimizing perplexity.
Perplexity, example
- random sequence of digits
- $p(x) = {1 \over 10}$
Perplexity is weighted branching factor.
Shannon’s game
Probability distribution for a next letter in a text depends on previous letters.
Some letters bear more information than the others (usually at the beginning of words).
When averaged, we have an estimation of entropy / perplexity of language.
What influences LM quality?
- size of training data
- order of language model
- smoothing
Large LM - n-gram counts
How many unique n-grams are in a corpus?
| order | types | singletons | % |
|---|---|---|---|
| unigram | 86,700 | 33,447 | (38,6%) |
| bigram | 1,948,935 | 1,132,844 | (58,1%) |
| trigram | 8,092,798 | 6,022,286 | (74,4%) |
| 4-gram | 15,303,847 | 13,081,621 | (85,5%) |
| 5-gram | 19,882,175 | 18,324,577 | (92,2%) |
Taken from Europarl with 30 mil. tokens.
Zero frequency, OOV, rare words
- probability must always be non zero
- to be able to measure perplexity
- maximum likelihood bad at it
- training data: work on Tuesday/Friday/Wednesday
- test data: work on Sunday,
$p(Sunday|work\ on) = 0$
Language models smoothing
We need to distinguish $p$ also for unseen data.
$$\forall w. p(w) > 0$$
The issue is more serious for high-order models.
Smoothing: amend ML of n-grams to expected counts in any data (different corpora).
Add-one smoothing (Laplace)
Maximum likelihood estimation assigns $p$ based on
$$p = \frac{c}{n}$$
Add-one smoothing uses
$$p = \frac{c+1}{n+v}$$
where $v$ is amount of all possible n-grams. All possible n-grams might outnumber real n-grams by several magnitudes.
Europarl has 139,000 types → 19 billion possible bigrams. In fact it has only 53 mil. tokens. How many bigrams?
This smoothing overvalues unseen n-grams.
Add-$\alpha$ smoothing
We won’t add 1, but $\alpha$. This can be estimated for the smoothing to be the most just and balanced.
$$p = \frac{c+\alpha}{n+\alpha v}$$
$\alpha$ can be obtained experimentally: we can try several different values and find the best one using perplexity.
Usually it is very small (0.000X).
Deleted estimation
We can find unseen n-grams in another corpus. N-grams contained in one of them and not in the other help us to estimate general amount of unseen n-grams.
E.g. bigrams not occurring in a training corpus but present in the other corpus million times (given the amount of all possible bigrams equals 7.5 billions) will occur approx. $$\frac{10^6}{7.5\times 10^9} = 0.00013\times$$
Good-Turing smoothing
We need to amend occurrence counts (frequencies) of n-grams in a corpus in such a way they correspond to general occurrence in texts. We use frequency of frequencies: number of n-grams which occur n×
We use frequency of hapax legomena (singletons in data) to estimate unseen data.
$$r^* = (r+1)\frac{N_{r+1}}{N_r}$$
Especially for n-grams not in our corpus we have $$r^*_0 = (0+1)\frac{N_1}{N_0} = 0.00015$$
where $N_1 = 1.1\times 10^6$ a $N_0 = 7.5\times 10^9$ (Europarl).
Missing f-of-f are smoothed.
Example of Good-Turing smoothing (Europarl)
| $c$ | FF | $c^*$ |
|---|---|---|
| 0 | 7,514,941,065 | 0.00015 |
| 1 | 1,132,844 | 0.46539 |
| 2 | 263,611 | 1.40679 |
| 3 | 123,615 | 2.38767 |
| 4 | 73,788 | 3.33753 |
| 5 | 49,254 | 4.36967 |
| 6 | 35,869 | 5.32929 |
| 8 | 21,693 | 7.43798 |
| 10 | 14,880 | 9.31304 |
| 20 | 4,546 | 19.54487 |
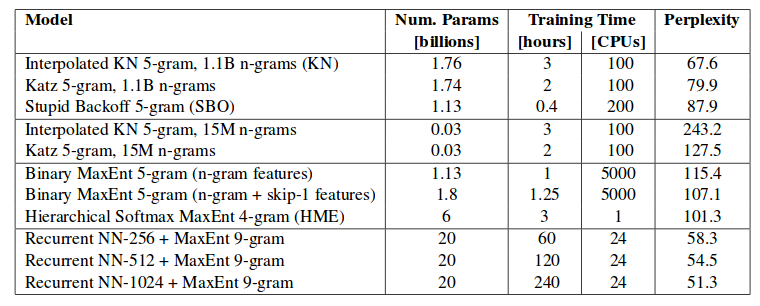
State-of-the-art
- Good-Turing
- Kneser-Ney (best for word n-grams)
- Witten-Bell (best for character n-grams)
Comparing smoothing methods (Europarl)
| method | perplexity |
|---|---|
| add-one | 382.2 |
| add-$\alpha$ | 113.2 |
| deleted est. | 113.4 |
| Good-Turing | 112.9 |
Close vs. open vocabulary tasks
- sometimes, V is known
- all other words are replaced with UNK
- easier for LM
Interpolation and back-off
Previous methods treated all unseen n-grams the same. Consider trigrams
nádherná červená řepa
nádherná červená mrkev
Despite we don’t have any of these in our training data, the former trigram should be more probable.
We will use probability of lower order models, for which we have necessary data:
červená řepa
červená mrkev
nádherná červená
Interpolation
$$p_I(w_3|w_1 w_2) = \lambda_1 p(w_3) \times \lambda_2 p(w_3|w_2) \times \lambda_3 p(w_3|w_1 w_2)$$
If we have enough data we can trust higher order models more and assign a higher significance to corresponding n-grams.
$p_I$ is probability distribution, thus this must hold: $$\forall\lambda_n:0 \le \lambda_n \le 1$$ $$\sum_n \lambda_n = 1$$
Stupid back-off
- non-normalized probabilities
- Large LM, Google 2007
- trillion words, billions of n-grams
- perplexity not available
- extrinsic evaluation possible (MT)
Cache language models
- recently used words are more likely to appear
- good for perplexity, not so good for WER (ASR)
$$p(w|h) = \lambda p(w_i|w_{i-2}w_{i-1}) + (1-\lambda) {c(w \in h) \over |h|}$$
Compressing language models
- quantize probabilities
- cut-off singletons
- entropy-based pruning
- efficient data structures: trie, suffix tree
Extrinsic evaluation: sentence completion
- Microsoft Research Sentence Completion Challenge
- evaluation of language models
- where perplexity not available
- from five Holmes novels
- training data: project Gutenberg
| Model | Acc |
|---|---|
| Human | 90 |
| simple 4-gram | 34 |
| smoothed 3-gram | 36 |
| simple character model | 38 |
| smoothed 4-gram | 39 |
| LSA probability | 49 |
| RNN | 59 |
| RMN (LSTM) | 69 |
Sentence completion
The stage lost a fine XXX, even as science lost an acute reasoner, when he became a specialist in crime.
a) linguist b) hunter c) actor d) estate e) horseman
What passion of hatred can it be which leads a man to XXX in such a place at such a time.
a) lurk b) dine c) luxuriate d) grow e) wiggle
My heart is already XXX since i have confided my trouble to you.
a) falling b) distressed c) soaring d) lightened e) punished
My morning’s work has not been XXX, since it has proved that he has the very strongest motives for standing in the way of anything of the sort.
a) invisible b) neglected c) overlooked d) wasted e) deliberate
That is his XXX fault, but on the whole he’s a good worker.
a) main b) successful c) mother’s d) generous e) favourite
Agreement completion challenge
- morphologically rich language: Czech
- data from czTenTen, heavily filtered
Údajně existuje studiová session, co jste nahrávalX s Iggy Popem.
ZtratilX téměř 5 kol a vyjíždělX pln odhodlání na dvanáctém místě.
Ahojte všechny, dnes jsme vstávalX brzy, páč se jelX na houby.
Sice jsem vyrůstalX v Plzni, ale Budějovice, to je moje první láska.
Pokud prodejce zaniklX a jeho živnost převzalX jiná firma, máte právo uplatnit reklamaci u této.
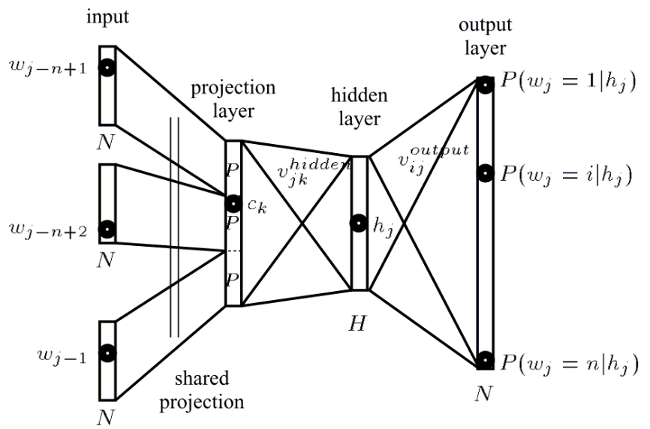
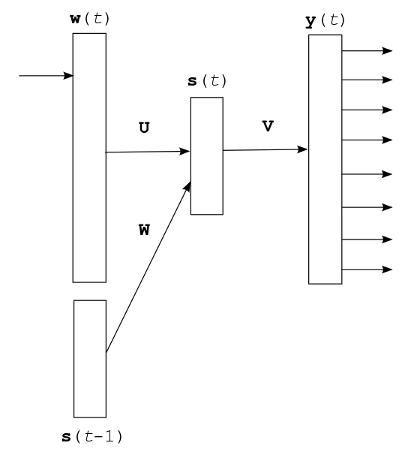
Neural network language models
- old approach (1940s)
- only recently applied successfully to LM
- 2003 Bengio et al. (feed-forward NNLM)
- 2012 Mikolov (RNN)
- trending right now
- key concept: distributed representations of words
- 1-of-V, one-hot representation
Feed-forward model
- fixed history (n)
- 1-of-V coding
Recurrent Neural Network
- Tomáš Mikolov (VUT)
- hidden layer feeds itself
- shown to beat n-grams by large margin
Word embeddings
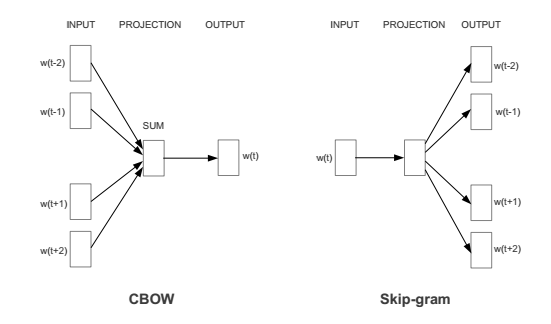
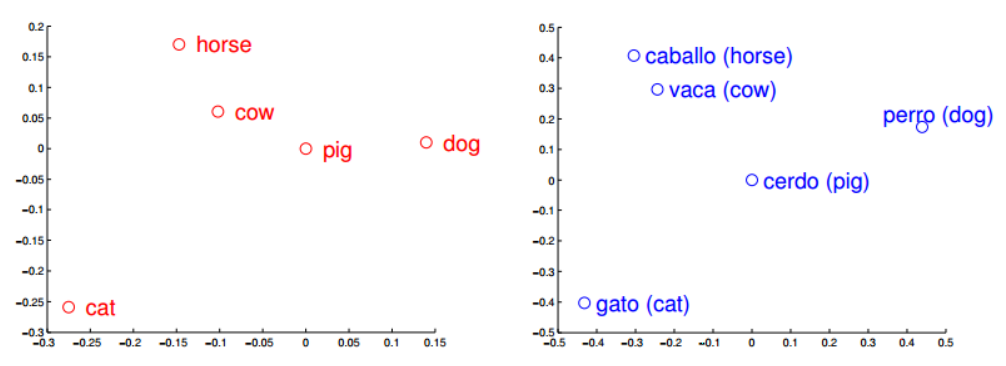
- distributional semantics with vectors
- skip-gram, CBOW (continuous bag-of-words)
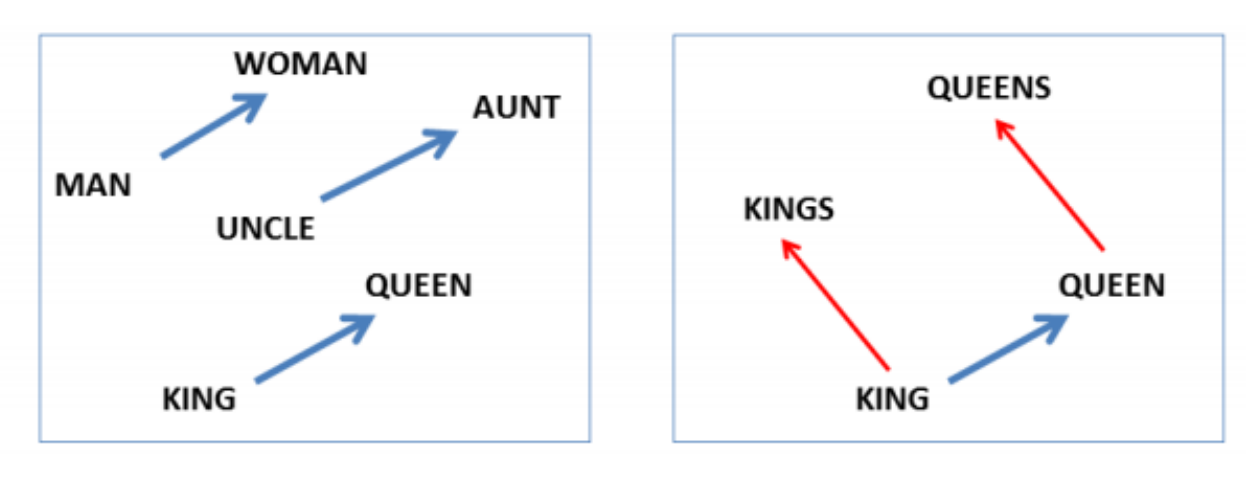
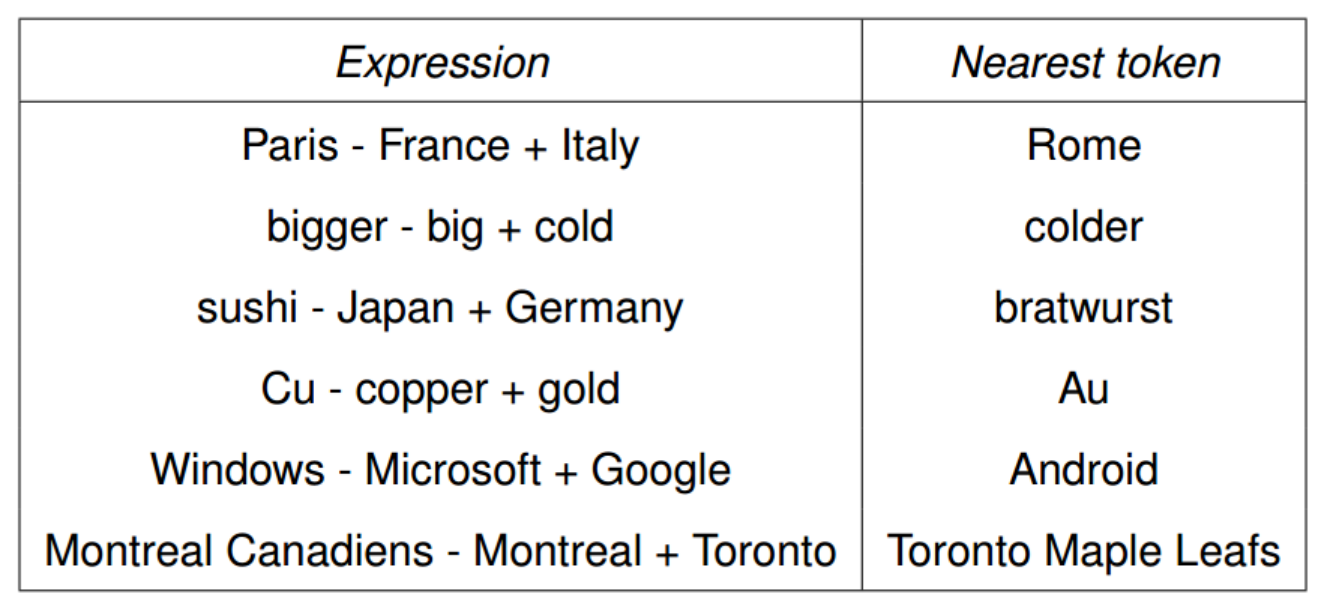
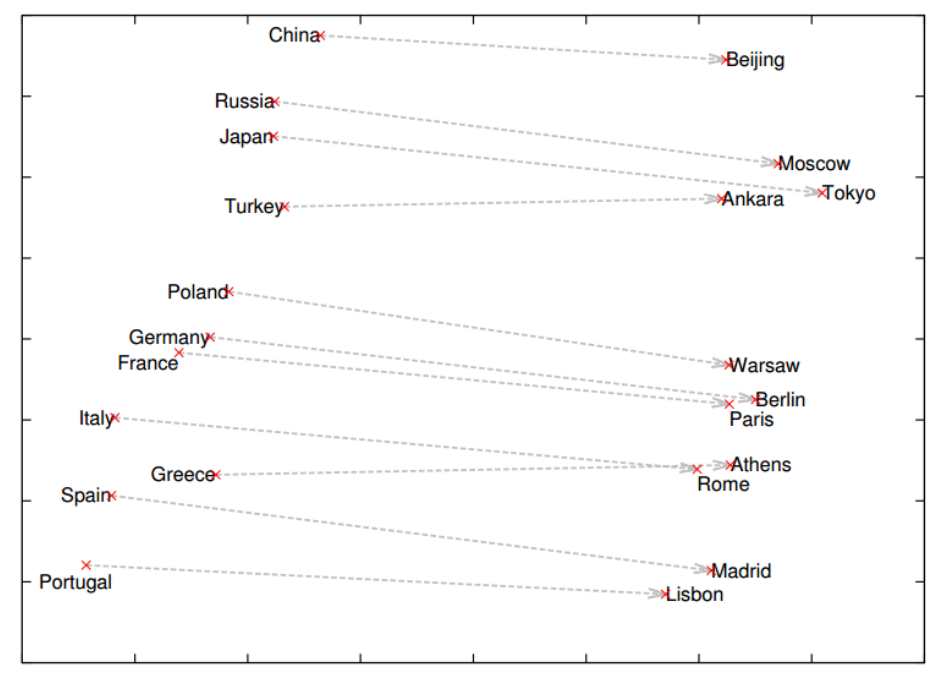
From Morpho-syntactic Regularities in Continuous Word Representations: A Multilingual Study (Nicolai, Cherry, Kondrak, 2015)
Long short-term memory
- RNN model, can learn to memorize and learn to forget
- beats RNN in sequence learning
- LSTM
Translation models
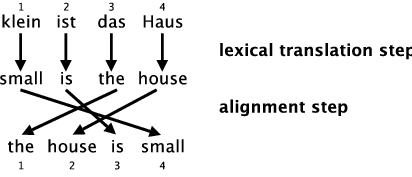
Lexical translation
Standard lexicon does not contain information about frequency of translations of individual meanings of words.
key → klíč, tónina, klávesa
How often are the individual translations used in translations?
key → klíč (0.7), tónina (0.18), klávesa (0.11)
probability distribution $p_f$: $$\sum_e p_f(e) = 1$$ $$\forall e: 0 \le p_f(e) \le 1$$
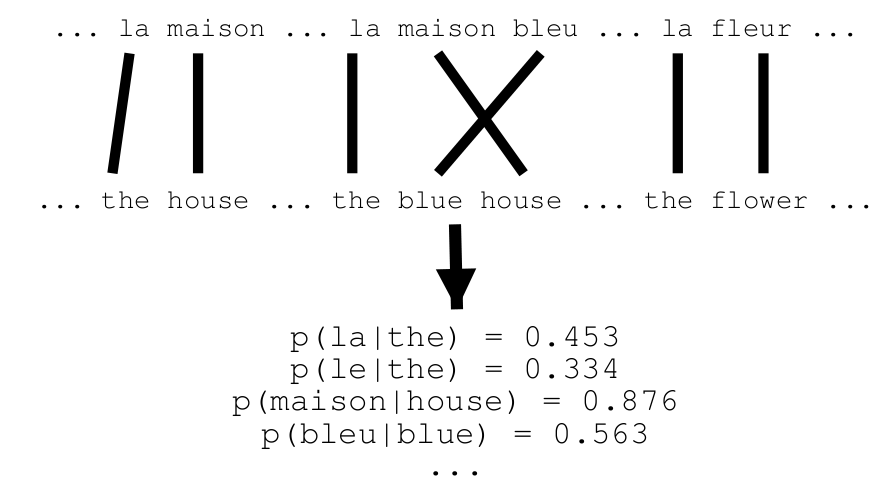
Word alignment, alignment function
Translations differ in number of words and in word order. SMT uses alignment function $$a:j\rightarrow i$$ where $j$ is position in TS, $i$ in SS.
| i: | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| the | castle | is | very | old | |
| ten | hrad | je | velmi | starý | |
| j: | 1 | 2 | 3 | 4 | 5 |
$a$ is function, therefore for each word $w_e$ from the target sentence there is exactly one word $w_f$ from the source sentence.
Word alignment: examples
- different word order:
it was written here
bylo to zde napsané
${1\rightarrow 2, 2\rightarrow 1, 3\rightarrow 4, 4\rightarrow 3}$ - different word number:
jsem maličký
i am very small
${1\rightarrow 1, 2\rightarrow 1, 3\rightarrow 2, 4\rightarrow 2}$ - no translational equivalents:
have you got it ?
máš to ? ${1\rightarrow 1, 2\rightarrow 4, 3\rightarrow 5}$ - the opposite case, we add token NULL, pozice 0:
NULL laugh
smát se
${1\rightarrow 1, 2\rightarrow 0}$
IBM model 1
$p_f$ not available. We split translation into several steps: generative modeling.
$$p(e, a|f) = \frac{\epsilon}{(l_f + 1)^{l_e}} \prod_{j=1}^{l_e} t(e_j|f_{a(j)})$$
where $e = (e_1, \dots e_{l_e})$ is target sentence, $f =(f_1, \dots f_{l_f})$ source sentence, $l_e$ is target sentence length, $l_f$ source sentence length, $\epsilon$ is normalizing constant, $(l_f + 1)^{l_e}$ is number of all possible alignments whereas $l_f$ is increased by $1$ due to NULL, $t$ is probability translation function.
Translation probability
For $p(e, a|f)$ we need $t$ for all words (pairs).
Parallel corpora with aligned sentences!
Word-level alignment in corpora (CEMAT) not available. Word-alignment by expectation-maximization (EM) algorithm.
EM algorithm
- expectation step, apply model to the data:
- parts of the model are hidden (alignments)
- using the model, assign probabilities to possible values
- maximization step, estimate model from data:
- take assigned values as fact
- collect counts (weighted by probabilities)
- estimate model from counts
- iterate until convergence
EM algorithm
- initialize the model (usually uniform distribution)
- apply model to the data (E step)
- adjust model according to the data (M step)
we amend word alignments count $w_e$ to $w_f$ (function $c$) according previous
$$c(w_e|w_f; e, f) = \sum_a p(a|e, f) \sum_{j=1}^{l_e}\delta(e, e_j)\delta(f, f_{a(j)})$$ where $\delta(x, y) = 1 \iff x == y$, else 0 - repeat E-M steps until the model can be improved
Translation probability in EM
$$t(w_e|w_f) = \frac{\sum_{(e,f)} c(w_e|w_f; e, f)}{\sum_{w_e} \sum_{(e, f)} c(w_e|w_f; e, f)}$$
EM algorithm - initialization

EM algorithm - final phase
IBM models
IBM-1 does not take context into account, cannot add and skip words. Each of the following models adds something more to the previous.
- IBM-1: lexical translation
- IBM-2: + absolute alignment model
- IBM-3: + fertility model
- IBM-4: + relative alignment model
- IBM-5: + further tuning
IBM-2
In IBM-1, all translations in different word order are of the same probability.
$p(e|f) = \sum_a p(e, a|f)$
IBM-2 adds explicit model of alignment: alignment probability distribution: $$a(i|j, l_w, l_f)$$ where $i$ is source word position, $j$ target word position.
IBM-2 – 2 steps of translation
Translation is split to two steps. In the first, lexical units are translated and in the second, words are rearranged according to the model.
IBM-2
The first step is the same as in IBM-1, $t(e|f)$ is used. Function $a$ with probability distribution $a$ is in the opposite direction to the translation direction. Both distributions are combined to formula for IBM-2:
$$p(e, a|f) = \epsilon \prod_{j=1}^{l_e} t(e_j|f_{a(j)}) a(a(j)|j, l_e, l_f)$$
$$p(e|f) = \sum_a p(e, a|f)$$ $$= \epsilon \prod_{j=1}^{l_e} \sum_{i=0}^{l_f} t(e_j|f_i) a(i|j, l_e, l_f)$$
IBM-3
Models 1 and 2 don’t consider situations where one word is translated to two and more words, or is not translated at all. IBM-3 solves this with fertility, which is modelled with a probability distribution $$n(\phi|f)$$
For each source word $f$, the distribution $n$ expresses, to how many words $f$ is usually translated.
$n(0|\hbox{a})$ = 0.999
$n(1|\hbox{king})$ = 0.997
$n(2|\hbox{steep})$ = 0.25
NULL token insertion
If we want to translate properly to a target language which uses words without translational equivalents we have to tackle with inserting NULL token.
$n(x|NULL)$ is not used since NULL insertion depends on a sentence length.
We add another step NULL insertion to the translation process. We use $p_1$ and $p_0 = 1 - p_1$, where $p_1$ stands for probability of NULL token insertion after any word in a sentence.
IBM-3
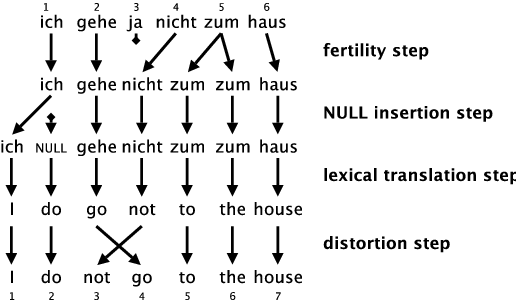
IBM-3 – distortion
The last step is almost the same as the 2. step in IBM-2 and is modelled with distortion probability distribution: $$d(j|i, l_e, l_f)$$
which models positions in an opposite direction: for each source word at position $i$ it models position $j$ of a target word.
IBM-3
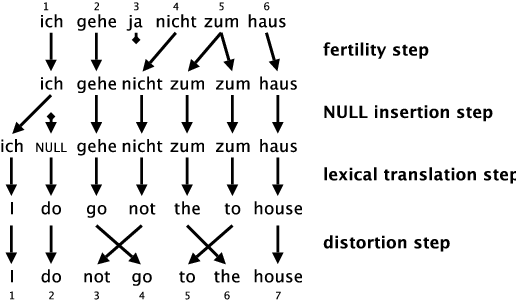
IBM-4
The problem of distortion lies in sparse data for long sentences. IBM-4 introduces relative distortion, where rearrangements of word positions depend on particular previous words. It comes from an assumption that we translate in phrases, which are moved together, or some rearrangement are more frequent (English: ADJ SUB → French SUB ADJ etc.).
IBM-5
solves other shortcomings of the previous models. E.g. it takes care of situations where two different source words could get to one target position (tracking of free positions).
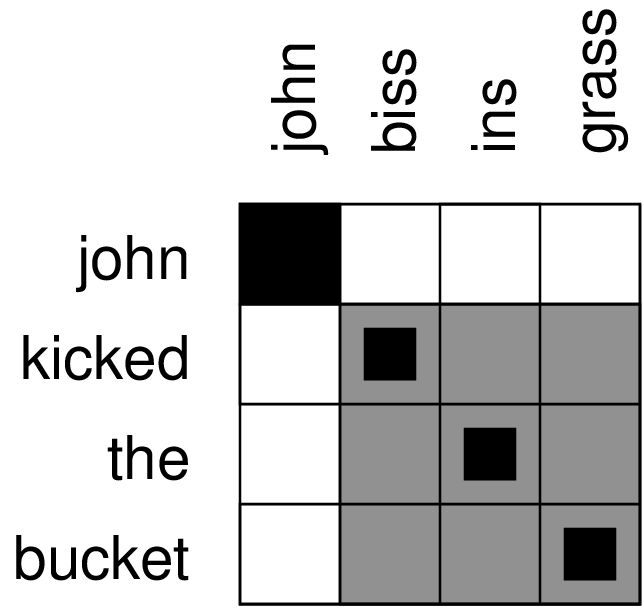
Word alignment matrix

Word alignment issues

Phrase-base Translation Model
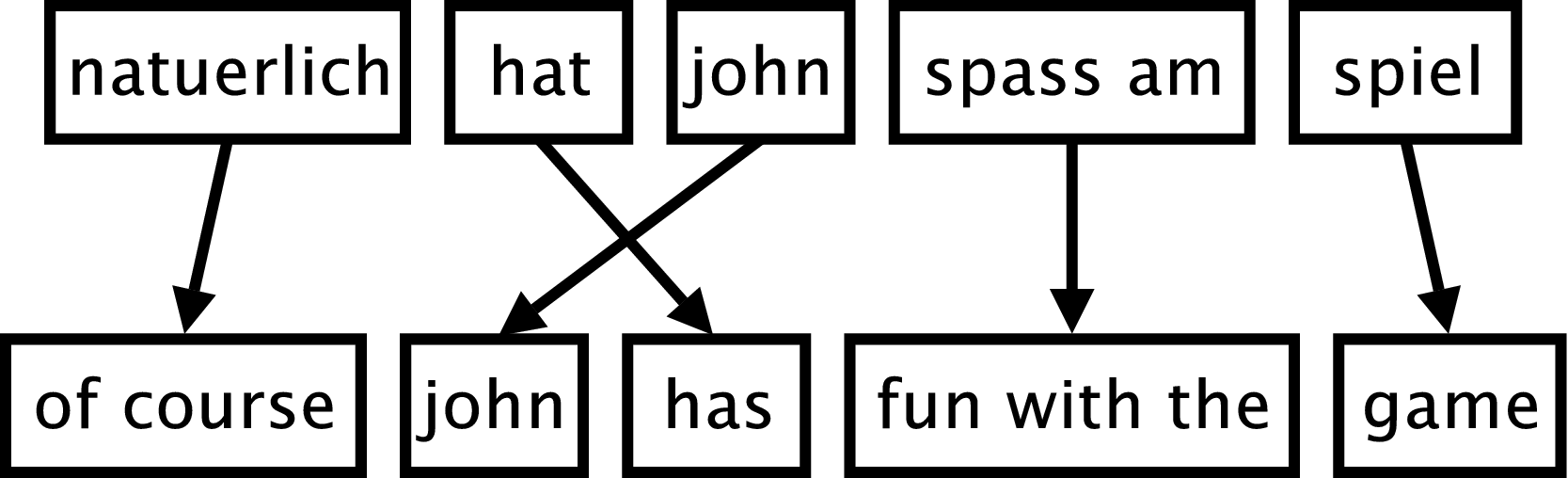
Phrases not linguistically, but statistically motivated. German am is seldom translated with single English to. Cf. (fun (with (the game)))
Advantages of PBTM
- translating n:m words
- word is not a suitable element for translation for many lang. pairs
- models learn to translate longer phrases
- simpler: no fertility, no NULL token etc.
Phrase-based model
Translation probability $p(f|e)$ is split to phrases:
$$ p(\bar{f}_1^I|\bar{e}1^I) = \prod{i=1}^I \phi(\bar{f}_i|\bar{e}i) d(start_i - end{i-1} - 1) $$
Sentence $f$ is split to $I$ phrases $\bar{f}_i$, all segmentations are of the same probability. Function $\phi$ is translation probability for phrases. Function $d$ is distance-based reordering model. $\hbox{start}_i$ is position of the first word of phrase from sentence $f$, which is translated to $i$-th phrase of sentence $e$.
Distance-based reordering model
- relative to a previous phrase
- minimal reordering is preferred
- the bigger reordering (measured on source side)
the less preferred is the operation
$$d(x) = \alpha^{abs(x)}$$
Reordering, example
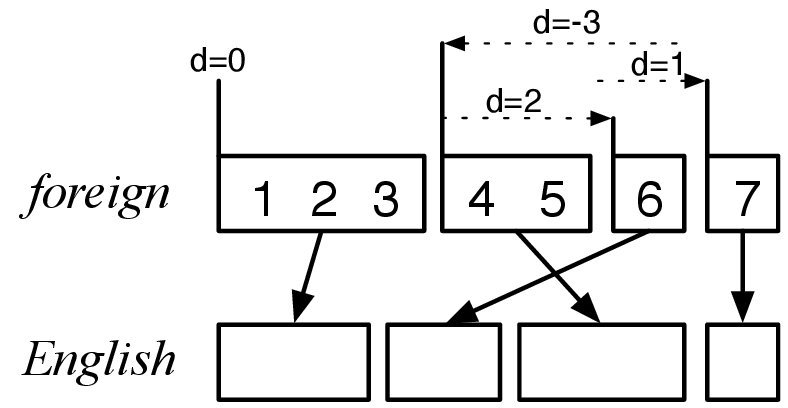
| phr | trans | move | d |
|---|---|---|---|
| 1 | 1-3 | at beg. | 0 |
| 2 | 6 | skip 4-5 | +2 |
| 3 | 4-5 | back over 4-6 | -3 |
| 4 | 7 | skip 6 | +1 |
Building phrase matrix
Re-use word alignments from EM algorithm.
Look for consistent phrases.
Phrase $\bar{f}$ and $\bar{e}$ are consistent with alignment $A$ if all words $f_1, \dots f_n$ in phrase $\bar{f}$, which have alignment in $A$, are aligned with words $e_1, \dots e_n$ in phrase $\bar{e}$ and vice versa.
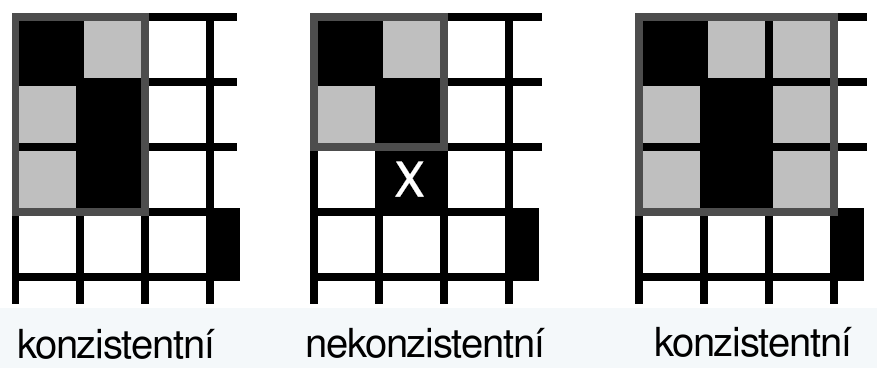
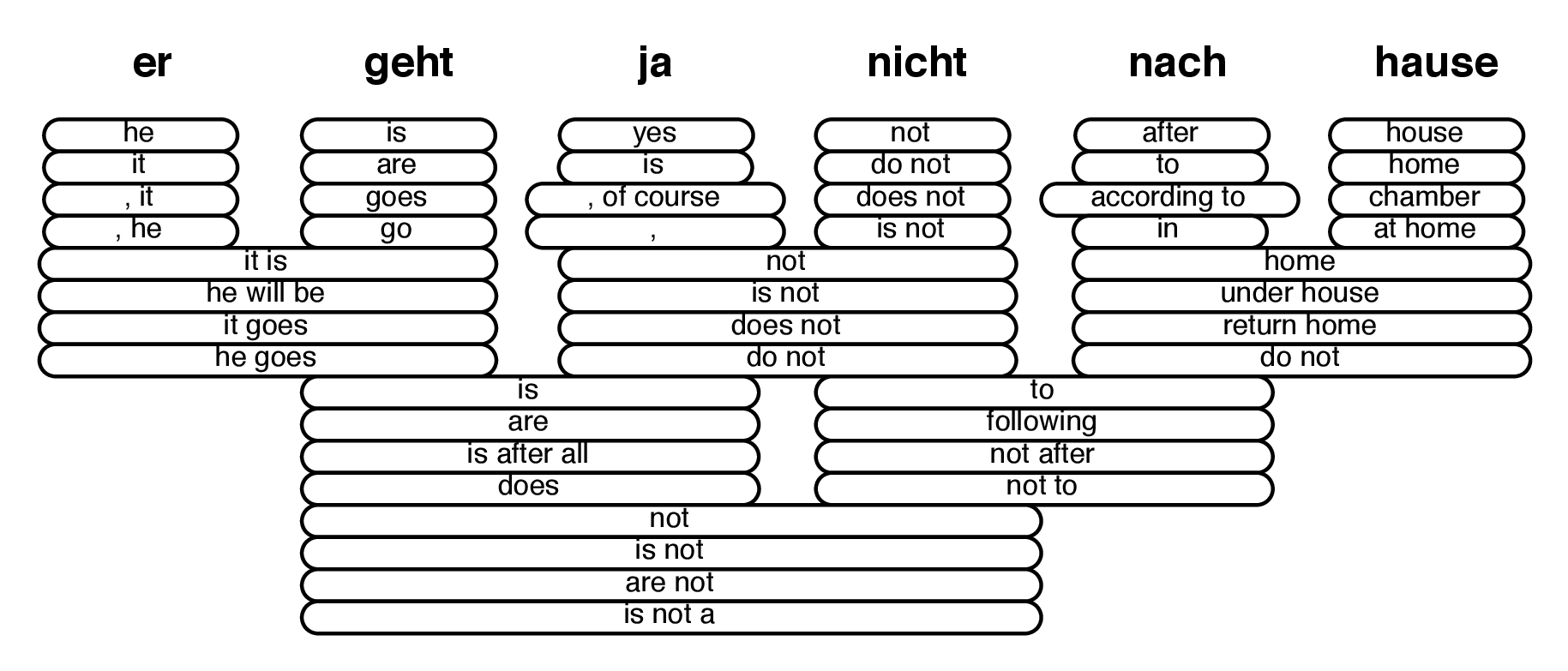
Phrase extraction

Extracted phrases
| phr1 | phr2 |
|---|---|
| michael | michael |
| assumes | geht davon aus / geht davon aus |
| that | dass / , dass |
| he | er |
| will stay | bleibt |
| in the | im |
| house | haus |
| michael assumes | michael geht davon aus / michael geht davon aus , |
| assumes that | geht davon aus , dass |
| assumes that he | geht davon aus , dass er |
| that he | dass er / , dass er |
| in the house | im haus |
| michael assumes that | michael geht davon aus , dass |
Phrase translation probability estimation
$$\phi(\bar{f}|\bar{e}) = \frac{\mbox{count}(\bar{e},\bar{f})}{\sum_{\bar{f_i}}\mbox{count}(\bar{e},\bar{f_i})} $$
Phrase-based model of SMT
$$e^* = \mbox{argmax}e \prod{i=1}^I \phi(\bar{f}i|\bar{e}i) ; d(start_i-end{i-1}-1)$$ $$\prod{i=1}^{|{\bf e}|} p_{LM}(e_i|e_1…e_{i-1})$$
Decoding
Given a model $p_{LM}$ and translation model $p(f|e)$ we need to find a translation with the highest probability but from exponential number of all possible translations.
Heuristic search methods are used.
It is not guaranteed to find the best translation.
Errors in translations are caused by
- decoding process, when the best translation is not found owing to the heuristics or
- models, where the best translation according to the probability functions is not the best possible.
Example of noise-induced errors (Google Translate)
- Rinneadh clárúchán an úsáideora yxc a eiteach go rathúil.
- The user registration yxc made a successful rejection.
- Rinneadh clárúchán an úsáideora qqq a eiteach go rathúil.
- Qqq made registration a user successfully refused.
Phrase-wise sentence translation
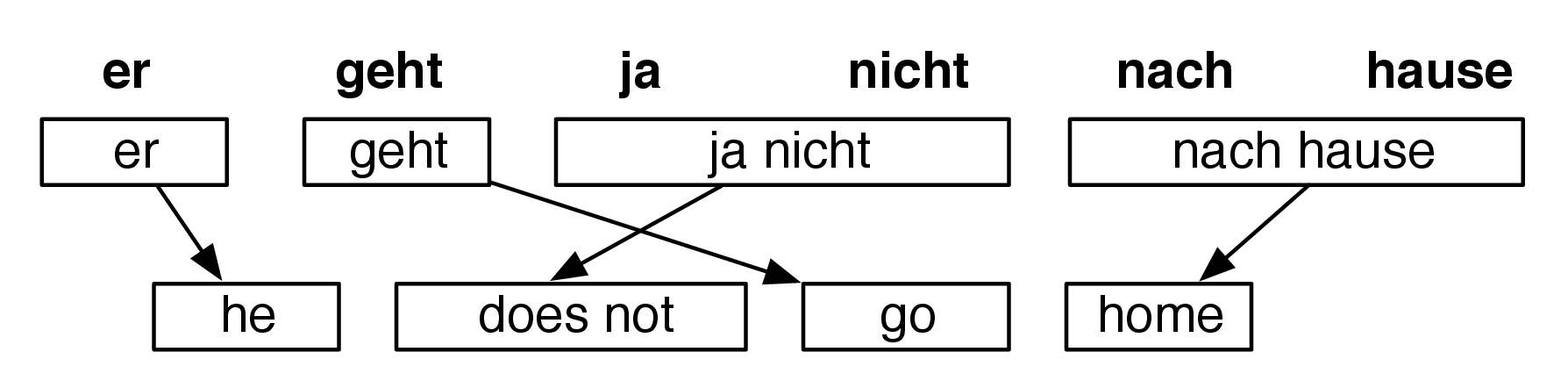
In each step of translation we count preliminary values of probabilities from the translation, reordering and language models.
Search space of translation hypotheses
Exponential space of all possible translations →
limit this space!
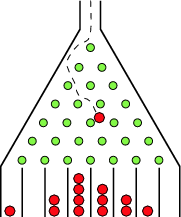
Hypothesis construction, beam search
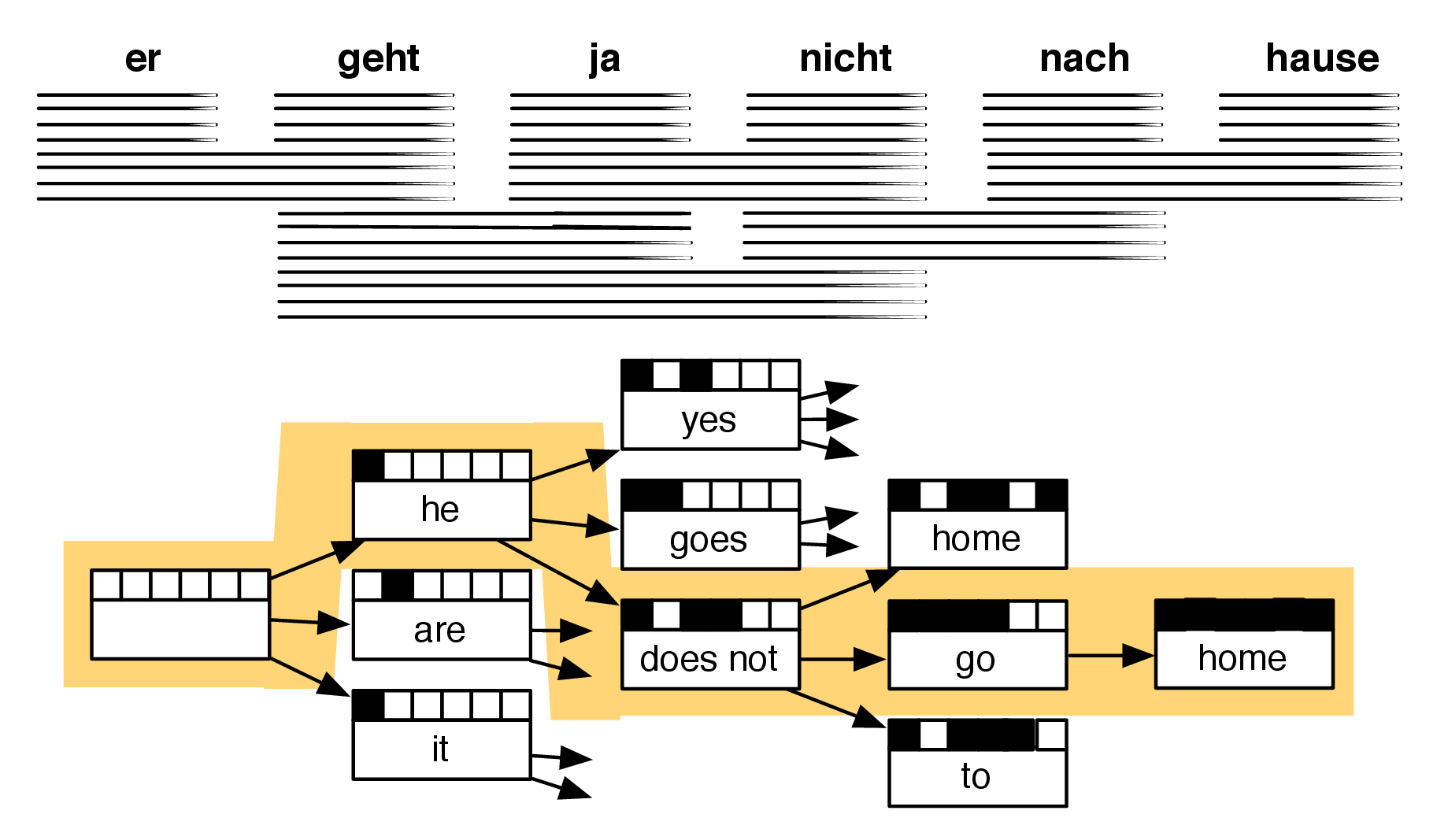
Beam search
- breadth-first search
- on each level of the tree:
generate all children of nodes on that level, sort them according to various heuristics - store only a limited number of the best states on each level (beam width)
- only these states are investigated further
- the wider beam the smaller number of children are pruned
- with an unlimited width → breadth-first search
- the width correlates with memory consumption
- the best final state might not be found since it can be pruned
Tools for SMT
- GIZA++: IBM models, word alignment (HMM)
- SRILM: language model toolkit
- IRST: large language model training
- Moses: phrase decoder, model training
- Pharaoh: beam search decoder for PBSMT
- Thot: phrase model training, online learning
- SAMT: tree-based models
Regular events
Annual evaluation of SMT quality. Test set preparing, manual evaluation events, etc.
- NIST: National Institute of Standards and Technology; the oldest, prestigious; evaluation of Arabic, Chinese
- IWSLT: international workshop of spoken language translation; speech translation, Asian languages
- WMT: Workshop on SMT; mainly EU languages
Neural network machine translation
- very close to state-of-the-art (PBSMT)
- a problem: variable length input and output
- learning to translate and align at the same time
- LISA
- hot topic (2014, 2015)
NN models in MT
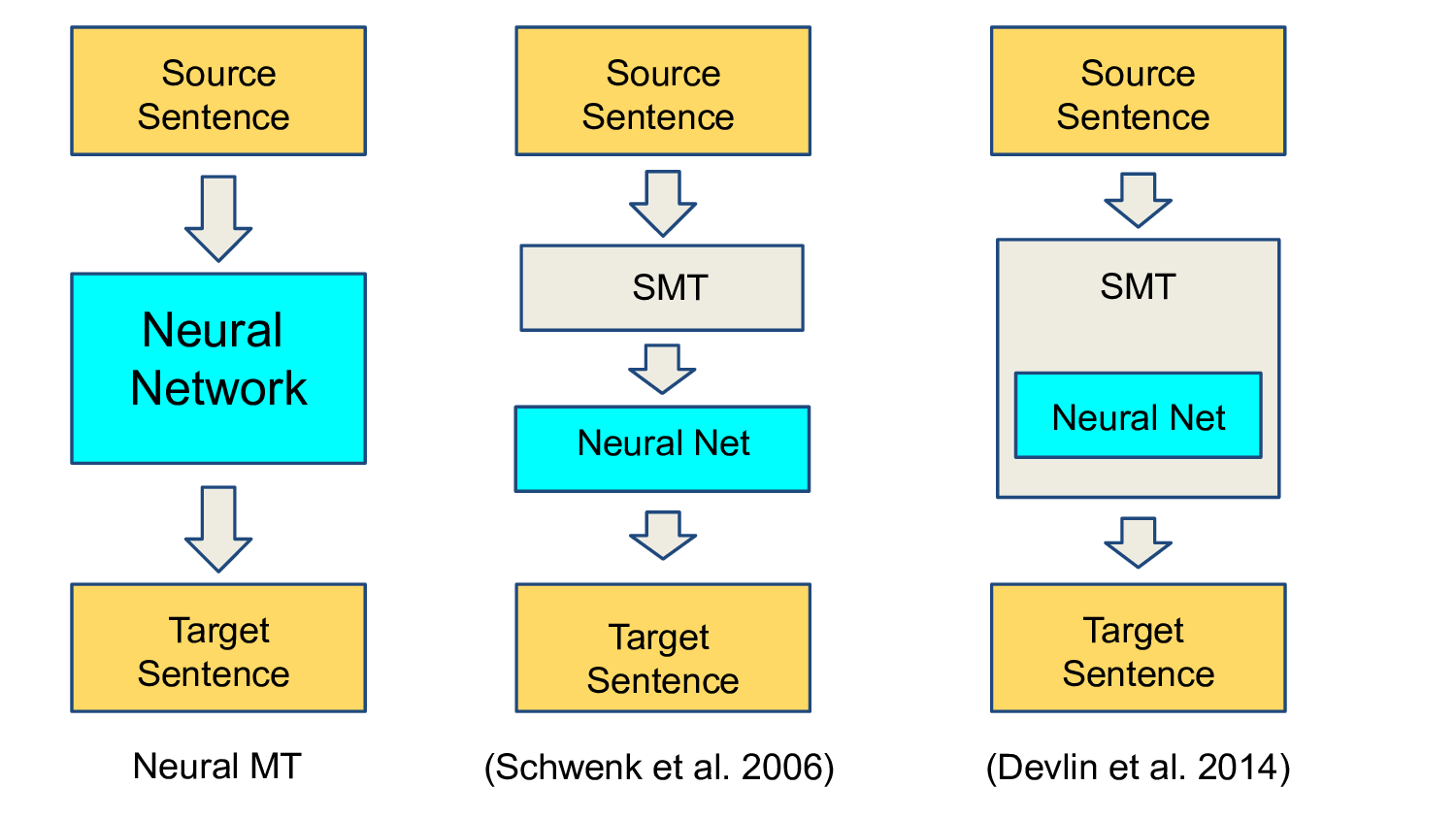
Encoder-decoder framework
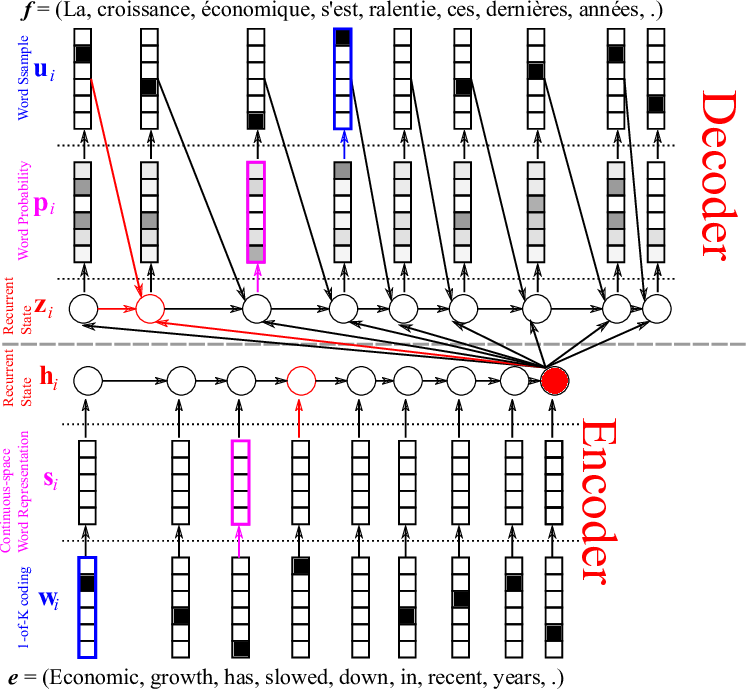
Summary vector for sentences
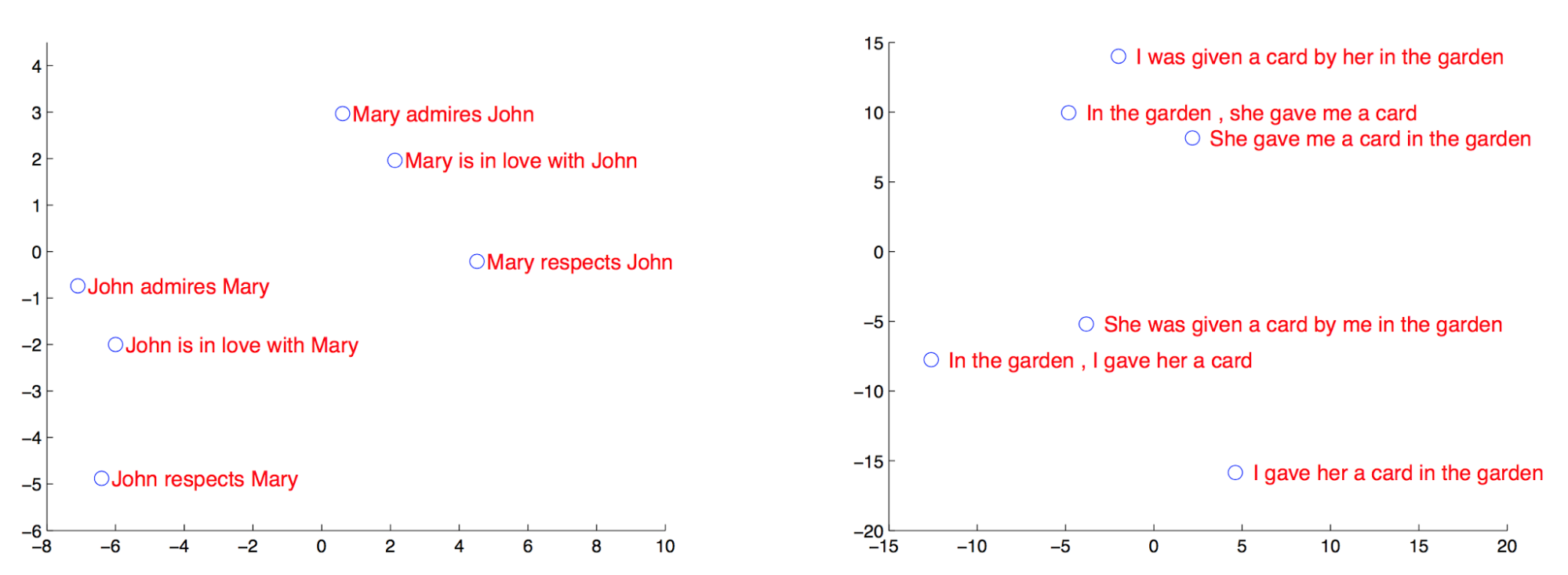
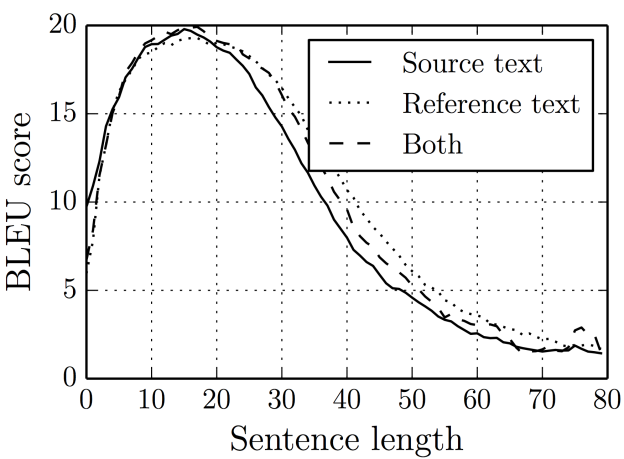
Problem with long sentences
Problem: any sentence is compressed to a fixed size vector.
Solution: bidirectional RNN + learning attention.
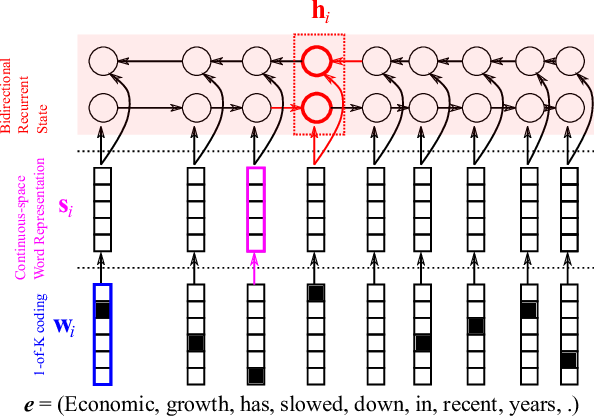
Bidirectional RNN
Attention mechanism
A neural network with a single hidden layer, a single scalar output
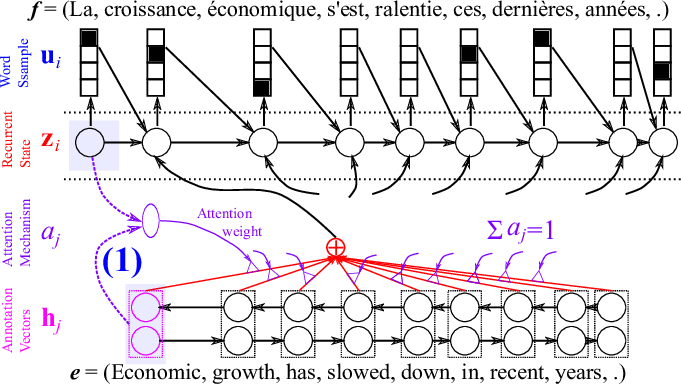
Alignment from attetion

Alignment with co-occurrence statistics
$$Dice = \frac{2 f_{xy}}{f_x + f_y}$$
$$logDice = 14 + \log_2 D$$
last modified: 2023-11-20
https://vit.baisa.cz/notes/learn/mt-stat/